Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a và SA vuông góc với đáy. Biết khoảng cách giữa AC và SB bằng a. Tính thể tích khối chóp S.ABCD A. 2 căn bậc hai của 2 a^3/3 B. 4
54
27/04/2024
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\) và \(SA\) vuông góc với đáy. Biết khoảng cách giữa \(AC\) và \(SB\) bằng \(a\). Tính thể tích khối chóp \(S.ABCD\).
A. \(\frac{{2\sqrt 2 {a^3}}}{3}\).
B. \(\frac{{4\sqrt 2 {a^3}}}{3}\).
C. \(\sqrt 2 {a^3}\).
D. \(\frac{{3{a^3}}}{{\sqrt 2 }}\).
Trả lời
Lời giải
Chọn B
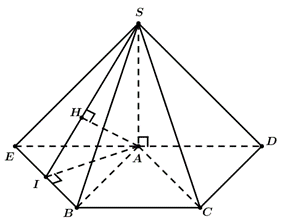
Dựng điểm \(E\) sao cho \(ACBE\) là hình bình hành.
Khi đó: \(AC//EB \Rightarrow AC//\left( {SBE} \right) \Rightarrow d\left( {AC,SB} \right) = d\left( {AC,\left( {SBE} \right)} \right) = d\left( {A,\left( {SBE} \right)} \right)\).
Kẻ \(AI \bot EB\left( {I \in AB} \right)\), kẻ \(AH \bot SI\left( {H \in SI} \right) \Rightarrow d\left( {A,\left( {SEB} \right)} \right) = AH = a\).
Tam giác \(A\) vuông tại tại \(A\).
Ta có \(\frac{1}{{A{I^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{4{a^2}}} = \frac{1}{{2{a^2}}}\).
Xét \(\Delta SAI\), ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}} \Leftrightarrow \frac{1}{{{a^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{2{a^2}}} \Leftrightarrow \frac{1}{{S{A^2}}} = \frac{1}{{2{a^2}}} \Rightarrow SA = a\sqrt 2 \).
Vậy thể tích của tích khối chóp \(S.ABCD\) là \({V_{S.ABCD}} = \frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{3}.a\sqrt 2 .4{a^2} = \frac{{4\sqrt 2 {a^3}}}{3}\).
