Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 60^0; SB = SC = SD = 2a. Tính thể tích khối chóp S.ABC A. a^3 căn bậc hai của 11} /24 B. a^3 căn bậc hai của 11/4 C. a^3 căn
55
05/05/2024
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \[a\], \(\widehat {BAD} = {60^0}\)\[SB = \,SC\, = \,SD\, = \,2a\]. Tính thể tích khối chóp \[S.ABC\].
A. \(\frac{{{a^3}\sqrt {11} }}{{24}}\).
B. \(\frac{{{a^3}\sqrt {11} }}{4}\).
C. \(\frac{{{a^3}\sqrt {11} }}{6}\).
D. \(\frac{{{a^3}\sqrt {11} }}{{12}}\).
Trả lời
Lời giải
Chọn B
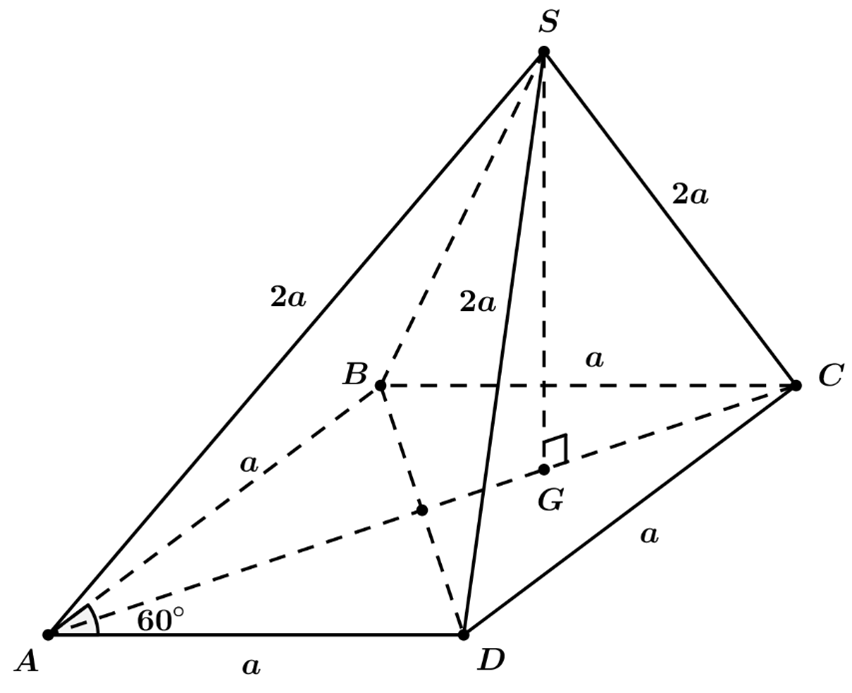
Vì \(ABCD\) là hình thoi và \(\widehat {BAD} = {60^0}\)nên tam giác \(ABD\) đều và tam giác \(BCD\) cũng đều.
Gọi \(G\) là tâm đường tròn ngoại tiếp tam giác \(BCD\) , vì\[\,SB = \,SC\, = \,SD\, = \,2a\] nên \(SG \bot \left( {BCD} \right)\).
Thể tích khối chóp \[{V_{S.ABC}} = \frac{1}{3}SG.{S_{ABC}}\].
\(SG = \sqrt {S{C^2} - C{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{2}{3}.\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{{a\sqrt {33} }}{3}\) .
\({S_{ABC}} = \frac{1}{2}{S_{ABCD}} = \frac{1}{2}\left( {2.\frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{{a^2}\sqrt 3 }}{4}\).
Vậy \[{V_{S.ABC}} = \frac{1}{3}SG.{S_{ABC}} = \frac{{{a^3}\sqrt {11} }}{4}\].

