Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a, BC = a căn bậc hai của 5, CD = a, góc giữa hai mặt phẳng ( SBC) và ( ABCD) bằng 60^0. Gọi I là trung điểm cạnh A
37
27/04/2024
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \[A\] và \(D\); \[AB = AD = 2a\], \[BC = a\sqrt 5 \], \[CD = a\], góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABCD} \right)\] bằng \[60^\circ \]. Gọi \[I\] là trung điểm cạnh \[AD\]. Biết hai mặt phẳng \(\left( {SBI} \right)\) và \[\left( {SCI} \right)\] cùng vuông góc với mặt phẳng \[\left( {ABCD} \right)\]. Tính thể tích khối chóp \[S.ABCD\].
A. \[V = \frac{{3\sqrt {15} {a^3}}}{5}\].
B. \[V = \frac{{{a^3}\sqrt {15} }}{5}\].
C. \[V = \frac{{{a^3}\sqrt {15} }}{{15}}\].
D. \[V = \frac{{3\sqrt {15} {a^3}}}{{15}}\].
Trả lời
Lời giải
Chọn A
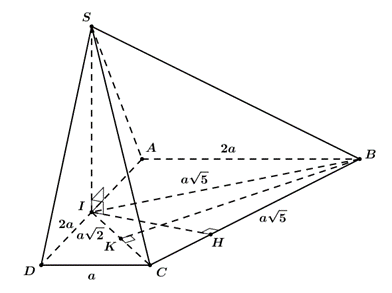
Do \[\left( {SBI} \right) \bot \left( {ABCD} \right)\] và \[\left( {SCI} \right) \bot \left( {ABCD} \right)\] nên \[SI \bot \left( {ABCD} \right)\].
Ta có \[IB = \sqrt {A{B^2} + A{I^2}} = a\sqrt 5 \], \[CI = \sqrt {C{D^2} + D{I^2}} = a\sqrt 2 \], suy ra tam giác \[BCI\] cân tại \[B\].
Gọi \[K\] là trung điểm của \[CI\], \[BK = \sqrt {B{C^2} - C{K^2}} = \sqrt {{{\left( {a\sqrt 5 } \right)}^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{3a\sqrt 2 }}{2}\], \[{S_{\Delta BCI}} = \frac{1}{2}BK.CI = \frac{{3{a^2}}}{2}\].
Kẻ \[IH \bot BC \Rightarrow BC \bot SH\] nên góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABCD} \right)\] là góc \[\widehat {SHI}\].
Mà \[{S_{\Delta BCI}} = \frac{1}{2}IH.BC \Rightarrow IH = \frac{{2{S_{\Delta BCI}}}}{{BC}} = \frac{{3a}}{{\sqrt 5 }}\], \[SI = IH.\tan 60^\circ = \frac{{3a}}{{\sqrt 5 }}.\sqrt 3 = \frac{{3a\sqrt {15} }}{5}\].
Vậy \[{V_{S.ABCD}} = \frac{1}{3}SI.{S_{ABCD}} = \frac{1}{3}\frac{{3a\sqrt {15} }}{5}\frac{{a + 2a}}{2}.2a = \frac{{3{a^3}\sqrt {15} }}{5}\].
