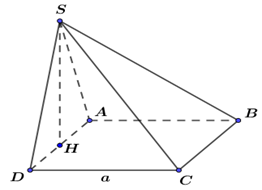
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, Delta SAD đều và mặt phẳng (SAD) vuông góc với mặt phẳng (ABC). Thể tích khối chóp S.ABCD bằng A. a^3 căn bậc hai của 3 /3 B. a^3
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, \[\Delta SAD\] đều và mặt phẳng (SAD) vuông góc với mặt phẳng (ABC). Thể tích khối chóp \(S.ABCD\) bằng
A. \[\frac{{{a^3}\sqrt 3 }}{3}\].
B. \[\frac{{{a^3}\sqrt 3 }}{2}\].
C. \[\frac{{{a^3}\sqrt 3 }}{6}\].
D. \[\frac{{{a^3}\sqrt 3 }}{4}\].