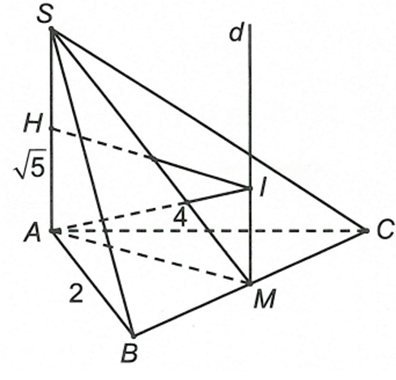
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và ab = 2, ac = 4, sa = căn bậc hai 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là
A.
B.
C.
D.