Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hai mặt phẳng ( SAB) và ( SAC) cùng vuông góc với đáy, góc tạo bởi ( SBC) và mặt đáy bằng 60^0. Thể tích khối chóp bằng A. a^3 căn bậc
76
27/04/2024
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với đáy, góc tạo bởi \(\left( {SBC} \right)\) và mặt đáy bằng \(60^\circ \). Thể tích khối chóp bằng
A. \(\frac{{{a^3}\sqrt 3 }}{4}\).
B. \(\frac{{{a^3}\sqrt 2 }}{8}\).
C. \(\frac{{3{a^3}\sqrt 3 }}{8}\).
D. \(\frac{{{a^3}\sqrt 3 }}{8}\).
Trả lời
Lời giải
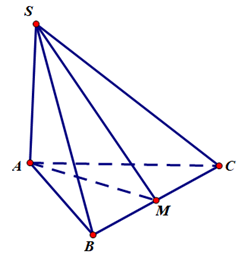
Từ giả thiết ta có \(\left\{ \begin{array}{l}\left( {SAB} \right)\, \bot \,\left( {ABC} \right)\\\left( {SAC} \right)\, \bot \,\left( {ABC} \right)\\\left( {SAB} \right)\, \cap \,\left( {SAC} \right) = SA\end{array} \right. \Rightarrow \,SA\, \bot \,\left( {ABC} \right)\).
Gọi \(M\) là trung điểm \(BC\). Do tam giác \(ABC\) đều nên \(BC\, \bot \,\left( {SAM} \right)\). Vậy \(\left( {\widehat {\left( {SBC} \right)\,;\,\left( {ABC} \right)}} \right) = \left( {\widehat {AM\,;\,SM}} \right)\, = \widehat {\,SMA}\, = 60^\circ \)
Do đó \(SA\, = \,AM\,.\tan 60^\circ \, = \,\frac{{3\,a}}{2}\)
Vậy thể tích khối chóp: \(V = \frac{1}{3}\,SA\,.\,{S_{\Delta ABC}} = \frac{1}{3}\,.\,\frac{{3\,a}}{2}\,.\,\frac{{{a^2}\,\sqrt 3 }}{4}\, = \,\frac{{{a^3}\,\sqrt 3 }}{8}\).

