Cho hàm số y = x^4 - 2x^2 - 3 có đồ thị như hình vẽ bên dưới. Với giá trị nào của tham số m thì phương trình x^4 - 2x^2 - 3 = 2m - 4 có hai nghiệm phân biệt? A. m nhỏ hơn bằng 1/2
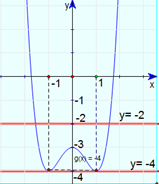
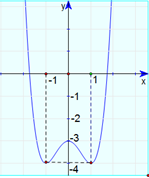
Cho hàm số \(y = {x^4} - 2{x^2} - 3\) có đồ thị như hình vẽ bên dưới. Với giá trị nào của tham số \(m\)thì phương trình \({x^4} - 2{x^2} - 3 = 2m - 4\) có hai nghiệm phân biệt?
A. \(m \le \frac{1}{2}\).
B. \(\left[ \begin{array}{l}m < 0\\m = \frac{1}{2}\end{array} \right.\).
C. \(0 < m < \frac{1}{2}\).
D. \(\left[ \begin{array}{l}m = 0\\m > \frac{1}{2}\end{array} \right.\).