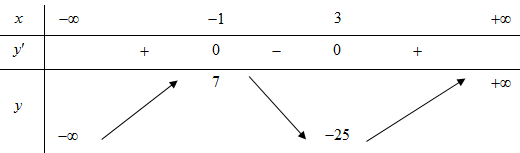Cho hàm số y = x^3 - 3x^2 - 9x + 2. Chọn kết luận đúng: A. Hàm số đạt cực tiểu tại x = 3. B. Hàm số đạt cực tiểu tại x = - 1. C. Hàm số đat cực tại tại x = 1 D. Hàm số đạt cực đại tại
Cho hàm số \[y = {x^3} - 3{x^2} - 9x + 2\]. Chọn kết luận đúng:
A. Hàm số đạt cực tiểu tại \[x = 3\].
B. Hàm số đạt cực tiểu tại \[x = - 1\].
C. Hàm số đat cực tại tại \[x = 1\].
D. Hàm số đạt cực đại tại \[x = 3\].