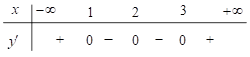Cho hàm số y = f( x ) thỏa mãn f'( x ) = ( x - 1)( x - 2)^2( x - 3), x thuộc R. Hàm số đã cho đạt cực đại tại A. x = 3 B.x = 2 C. x = 1 D. x = - 1
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f'\left( x \right) = \left( {x - 1} \right){\left( {x - 2} \right)^2}\left( {x - 3} \right)\), \(\forall x \in \mathbb{R}\). Hàm số đã cho đạt cực đại tại
A. \(x = 3\).
B.\(x = 2\).
C.\(x = 1\).
D.\(x = - 1\).