Cho hàm số y = f( x ) liên tục trên R và có đạo hàm f'( x ) = x^3( x - 4)( x - 1)^2. Hàm số y = f( x^2) nghịch biến trên những khoảng nào sau đây? A. ( - 2; 0). B. ( - vô cùng ; - 2)
70
04/05/2024
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right)\; = {x^3}\left( {x - 4} \right){\left( {x - 1} \right)^2}\). Hàm số \(y = f\left( {{x^2}} \right)\) nghịch biến trên những khoảng nào sau đây?
A. \(\left( { - 2\;;\;0} \right)\).
B. \(\left( { - \infty ; - 2} \right)\).
C. \(\left( {2\;;\; + \infty } \right)\).
D. \(\left( { - 1\;;\;1} \right)\).
Trả lời
Lời giải
Chọn B
\(y' = {\left[ {f\left( {{x^2}} \right)} \right]^'} = \;2x.f'\left( {{x^2}} \right) = 2x{\left( {{x^2}} \right)^3}\left( {{x^2} - 4} \right){\left( {{x^2} - 1} \right)^2} = 2{x^7}\left( {{x^2} - 4} \right){\left( {x - 1} \right)^2}{\left( {x + 1} \right)^2}\).
\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{x = 0\;\;\;\left( {{\rm{boi}}7} \right)}\\{x = 2\;\;\;\left( {{\rm{boi}}1} \right)}\end{array}}\\{x = - 2\;\left( {{\rm{boi}}1} \right)}\\{x = 1\;\;\;\;\left( {{\rm{boi}}2} \right)}\end{array}}\\{\;x = - 1\;\left( {{\rm{boi}}2} \right)}\end{array}} \right.\)
Ta có bảng biến thiên của hàm số \(y = f\left( {{x^2}} \right)\) như sau:
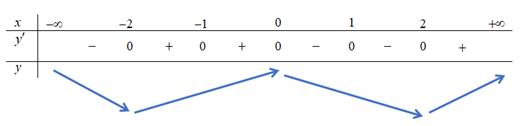
Vậy hàm số \(y = f\left( {{x^2}} \right)\) nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\).

