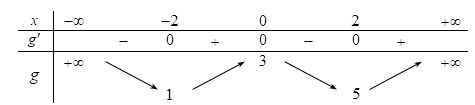Cho hàm số y = f( x ) liên tục trên R có đồ thị hàm số y = f'( x ) như hình vẽ. Xét hàm số g( x ) = f( x ) - 1/2x^2 - 3x. Khi đó khẳng định nào sau đây đúng ? A. g( 0 ) nhỏ hơn bằng g( 2 )
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ.
Xét hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} - 3x\). Khi đó khẳng định nào sau đây đúng ?
A. \(g\left( 0 \right) \le g\left( 2 \right)\).
B. \(g\left( { - 2} \right) > g\left( 0 \right)\).
C. \(g\left( 2 \right) < g\left( 4 \right)\).
D. \(g\left( { - 4} \right) = g\left( { - 2} \right)\).