Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau

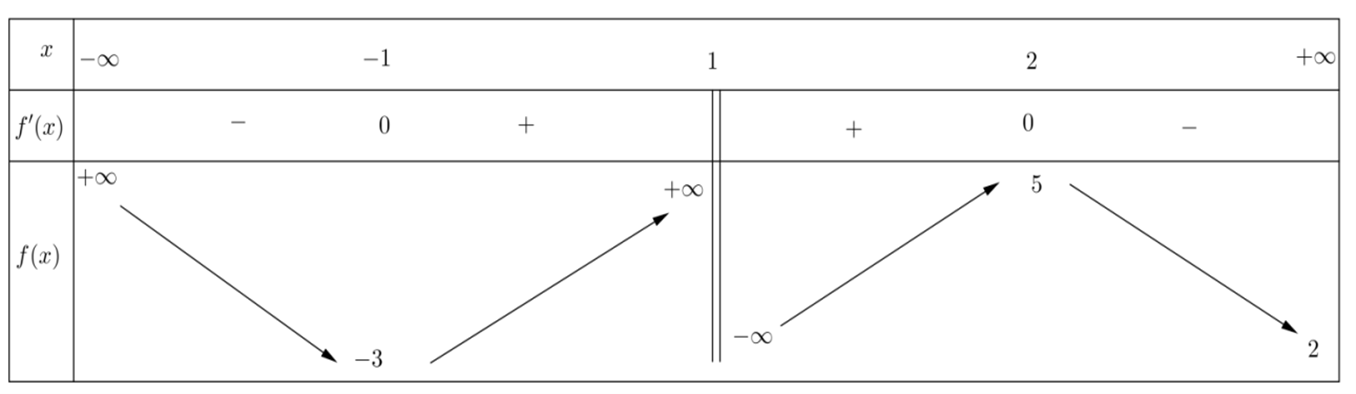
Số đường tiệm cận đứng của đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{f\left( x \right) - 3}}\).

Chọn D

Dựa vào bảng biến thiên ta có:

Phương trình \(f\left( x \right) - 3 = 0\) \( \Leftrightarrow f\left( x \right) = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = a \in \left( { - \infty ; - 1} \right)}\\{x = b \in \left( { - 1;1} \right)}\\{x = c \in \left( {1;2} \right)}\\{x = d \in \left( {2; + \infty } \right)}\end{array}} \right.\).

\(\mathop {lim}\limits_{x \to {a^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {a^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = - \infty \Rightarrow \) đường thẳng \(x = a\) là đường tiệm cận đứng. \(\mathop {lim}\limits_{x \to {b^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {b^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = + \infty \) \( \Rightarrow \) đường thẳng \(x = b\) là đường tiệm cận đứng.

\(\mathop {lim}\limits_{x \to {c^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {c^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = + \infty {\rm{\;}} \Rightarrow \)đ ường thẳng \(x = c\) là đường tiệm cận đứng.

\(\mathop {lim}\limits_{x \to {d^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {d^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = - \infty \) \( \Rightarrow \) đường thẳng \(x = d\) là đường tiệm cận đứng.

Vậy đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{f\left( x \right) - 3}}\) có 4 đường tiệm cận đứng.