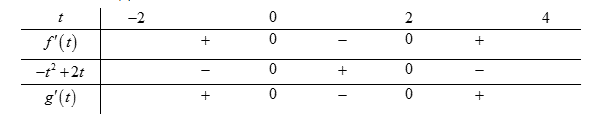Cho hàm số y = f( x ) liên tục, có đạo hàm trên [ - 2;4] và có bảng biến thiên như hình vẽ Số nghiệm của phương trình 3f( - 2x + 1) = 8x^3 - 6x trên đoạn [ - 3/2; 3/2] là A. 3 B. 5
37
04/05/2024
Cho hàm số \(y = f\left( x \right)\)liên tục, có đạo hàm trên \(\left[ { - 2;4} \right]\)và có bảng biến thiên như hình vẽ
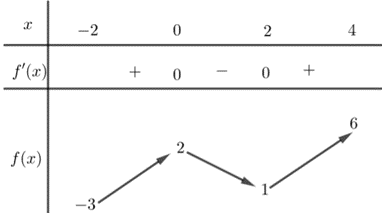
Số nghiệm của phương trình \(3f\left( { - 2x + 1} \right) = 8{x^3} - 6x\) trên đoạn \(\left[ {\frac{{ - 3}}{2};\frac{3}{2}} \right]\) là
A. \(3\).
B. \(5\).
C. \(1\).
D. \(2\).
Trả lời
Lời giải
Chọn C
Đặt \(t = - 2x + 1\).Với \(x \in \left[ {\frac{{ - 3}}{2};\frac{3}{2}} \right] \Rightarrow t \in \left[ { - 2;4} \right]\).
Mỗi nghiệm của \(t\) cho duy nhất một nghiệm của \(x\).
Biến đổi \(8{x^3} - 6x = {\left( {2x} \right)^3} - 3\left( {2x} \right) = {\left( {1 - t} \right)^3} - 3\left( {1 - t} \right) = - {t^3} + 3{t^2} - 2\).
Phương trình trở thành \(3f\left( t \right) - \left( { - {t^3} + 3{t^2} - 2} \right) = 0\).
Xét hàm số
\(g\left( t \right) = 3f\left( t \right) - \left( { - {t^3} + 3{t^2} - 2} \right)\) \( \Rightarrow g'\left( t \right) = 3f'\left( t \right) - \left( { - 3{t^2} + 6t} \right) = 3\left[ {f'\left( t \right) - \left( { - {t^2} + 2t} \right)} \right]\)
\(g'\left( t \right) = 0 \Leftrightarrow f'\left( t \right) = - {t^2} + 2t\)
Ta có \(f'\left( t \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
\( - {t^2} + 2t = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Ta có bảng xét dấu \(g'\left( t \right)\)
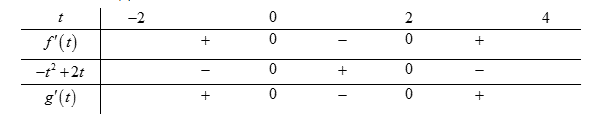
Từ đó ta có bảng biến thiên sau:
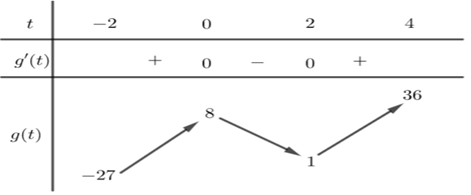
Dựa vào bảng biến thiên ta có phương trình \(g\left( t \right) = 0\) có \(1\) nghiệm nên phương trình ban đầu có \(1\) nghiệm.