Cho hàm số y = f( x ) có đồ thị hàm số y = f( | x|) như hình vẽ Chọn kết luận đúng trong các kết luận sau: A. f( x ) = - x^3 + x^2 + 4x - 4 B. f( x ) = x^3 - x^2 - 4x + 4 C. f( x ) =
58
27/04/2024
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như hình vẽ
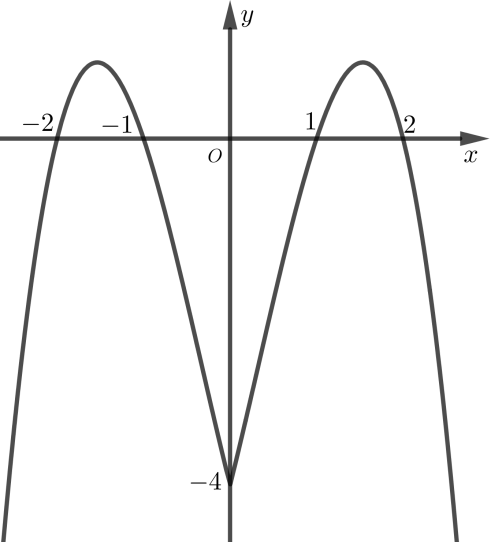
Chọn kết luận đúng trong các kết luận sau:
A. \(f\left( x \right) = - {x^3} + {x^2} + 4x - 4\)
B. \(f\left( x \right) = {x^3} - {x^2} - 4x + 4\)
C. \(f\left( x \right) = - {x^3} - {x^2} + 4x + 4\)
D. \(f\left( x \right) = {x^3} + {x^2} - 4x - 4\)
Trả lời
Lời giải
Chọn A
Cách 1:
Ta đã biết từ đồ thị \(\left( C \right)\):\(y = f\left( x \right)\) suy ra đồ thị \(\left( {{C_1}} \right)\):\(y = f\left( {\left| x \right|} \right)\) sẽ gồm hai phần.
\( \oplus \) Phần 1: Giữ nguyên phần đồ thị \(\left( C \right)\) ở bên phải trục tung.
\( \oplus \) Phần 2: Bỏ phần đồ thị \(\left( C \right)\) bên trái trục tung và lấy đối xứng phần 1 qua trục tung.
Từ dáng điệu của đồ thị đã cho ta quan sát phần đồ thị bên phải có ngay được:
\( \oplus \) \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow y = f\left( x \right)\) có hệ số \(a < 0\)
\( \oplus \) Đồ thị hàm số cắt trục tung tại một điểm có tung độ âm nên \(y = f\left( x \right)\) có hệ số \(d < 0\).
Vậy đáp án A.
Cách 2:
Nhận xét đồ thị đi qua điểm \(A\left( {1;0} \right)\), \(B\left( {0; - 4} \right)\) , \(C\left( {2;0} \right)\) nên ta kiểm tra các đáp án
Ta có \( - {1^3} + {1^2} + 4.1 - 4 = 0\); \( - {0^3} + {0^2} + 4.0 - 4 = - 4\); \( - {2^3} + {2^2} + 4.2 - 4 = 0\)nên \(A\left( {1;0} \right)\), \(B\left( {0; - 4} \right)\) , \(C\left( {2;0} \right)\) thuộc \(y = f\left( x \right) = - {x^3} + {x^2} + 4x - 4\) .

