Cho hàm số y = f( x ) có đạo hàm liên tục trên R. Đồ thị hàm số y = f'( x ) như hình bên dưới. Hỏi hàm số g( x ) = 2f( 2 - x/2) + x^2/4 - 2x + 2020 nghịch biến trên khoảng nào trong các k
35
04/05/2024
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới.
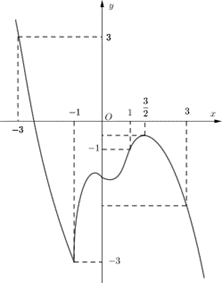
Hỏi hàm số \(g\left( x \right) = 2f\left( {2 - \frac{x}{2}} \right) + \frac{{{x^2}}}{4} - 2x + 2020\) nghịch biến trên khoảng nào trong các khoảng sau ?
A. \(\left( {2;\,3} \right)\).
B. \(\left( {\, - 1;\,3} \right)\).
C. \(\left( { - 2;\,3} \right)\).
D. \(\left( {10;\, + \infty } \right)\).
Trả lời
Lời giải
Chọn A
Ta có \(g\left( x \right) = 2f\left( {2 - \frac{x}{2}} \right) + \frac{{{x^2}}}{4} - 2x + 2020 \Rightarrow g'\left( x \right) = - f'\left( {2 - \frac{x}{2}} \right) + \frac{x}{2} - 2\)
Đặt \(t = 2 - \frac{x}{2} \Rightarrow x = 4 - 2t\)
Suy ra \(g'\left( {4 - 2t} \right) = - f'\left( t \right) - t\)
\(g'\left( {4 - 2t} \right) = 0 \Leftrightarrow f'\left( t \right) = - t\,\left( * \right)\)
Phương trình (*) là phương trình trình hoành độ giao điểm của đồ thị hàm số \(f'\) và đường thẳng \(y = - x\).
Dựa vào đồ thị:
\(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}t = - 3\\t = 1\\t = 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = 10\\x = 2\\x = - 2\end{array} \right.\)
Ta có bảng xét dấu của hàm \(g'\)
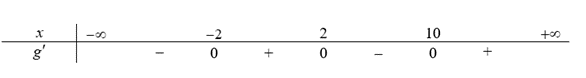
\(g(x)\) nghịch biến trên khoảng \(\left( {2;10} \right)\)nên nghịch biến trên khoảng \(\left( {2;\,3} \right)\).