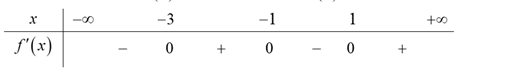Cho hàm số y = f( x ), có bảng xét dấu f'( x ) như sau: Hàm số y = f( 3 - 2x ) đồng biến trên khoảng nào dưới đây? A. ( 3; + vô cùng). B. ( 2; 4). C. ( 1; + vô cùng). D. ( - v
47
25/04/2024
Cho hàm số \(y = f\left( x \right)\), có bảng xét dấu \(f'\left( x \right)\) như sau:
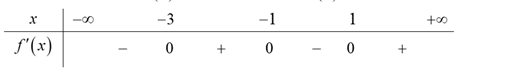
Hàm số \(y = f\left( {3 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
A. \(\left( {3\,;\, + \infty } \right)\).
B. \(\left( {2\,;\,4} \right)\).
C. \(\left( {1\,;\, + \infty } \right)\).
D. \(\left( { - \infty \,;\,1} \right)\).
Trả lời
Lời giải
Chọn A
Xét hàm số \(y = g\left( x \right) = f\left( {3 - 2x} \right)\).
Ta có \(g'\left( x \right) = - 2f'\left( {3 - 2x} \right)\). Suy ra \[g'\left( x \right) = - 2f'\left( {3 - 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3 - 2x = - 3\\3 - 2x = - 1\\3 - 2x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 2\\x = 1\end{array} \right.\].
Ta có bảng xét dấu \(g'\left( x \right)\) như sau:

Từ bảng xét dấu của \(g'\left( x \right)\) suy ra hàm số \(y = f\left( {3 - 2x} \right)\) đồng biến trên khoảng \(\left( {3\,;\, + \infty } \right)\).