Cho hàm số y = f( x ) có bảng xét dấu đạo hàm như sau: Hàm số y = 3f( x + 3) - x^3 + 12x nghịch biến trên khoảng nào sau đây? A. ( - vô cùng ; - 1). B. ( - 1;0). C. ( 1;5). D. (
36
30/04/2024
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng nào sau đây?
A. \(\left( { - \infty ; - 1} \right)\).
B. \(\left( { - 1;0} \right)\).
C. \(\left( {1;5} \right)\).
D. \(\left( {2; + \infty } \right)\).
Trả lời
Lời giải
Chọn D
Ta có \(y' = 3f'\left( {x + 3} \right) - 3{x^2} + 12 = 3\left[ {f'\left( {x + 3} \right) + \left( {4 - {x^2}} \right)} \right]\)
Từ bảng xét dấu của \(f'\left( x \right)\) ta có \(f'\left( {x + 3} \right) < 0 \Leftrightarrow \left[ \begin{array}{l} - 1 < x + 3 < 1\\5 < x + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 4 < x < - 2\\x > 2\end{array} \right.\);
\(f'\left( {x + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 4\\x = \pm 2\end{array} \right.\).
Suy ra bảng xét dấu \(y'\) như sau
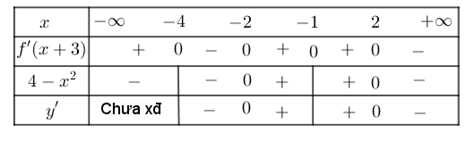
Vậy hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng \(\left( {2; + \infty } \right)\) và \(\left( { - 4; - 2} \right)\).


