Cho hàm số y = f( x ) có bảng biến thiên như hình vẽ. Phương trình 2| f( x )| = 1 có bao nhiêu nghiệm nhỏ hơn 2? A. 4 B. 2 C. 6 D. 3
45
04/05/2024
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ.
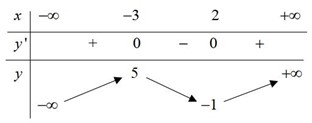
Phương trình \(2\left| {f\left( x \right)} \right| = 1\) có bao nhiêu nghiệm nhỏ hơn 2?
A. \(4\).
B. \(2\).
C. \(6\).
D. \(3\).
Trả lời
Lời giải
Chọn A
Ta có \(2\left| {f\left( x \right)} \right| = 1 \Leftrightarrow \left| {f\left( x \right)} \right| = \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = \frac{1}{2}}\\{f\left( x \right) = - \frac{1}{2}}\end{array}} \right.\).
Từ bảng biến thiên của hàm số \(y = f\left( x \right)\) ta có:
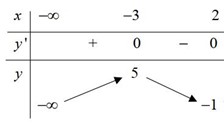
+) Phương trình \(f\left( x \right) = \frac{1}{2}\) có 2 nghiệm nhỏ hơn 2.
+) Phương trình \(f\left( x \right) = - \frac{1}{2}\) có 3 nghiệm nhỏ hơn 2.
Vậy phương trình \(2\left| {f\left( x \right)} \right| = 1\) có bốn nghiệm nhỏ hơn 2.


