Cho hàm số y = f( x ) có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và ngang? A. 3 . B. 1. C. 2. D. 4.
39
27/04/2024
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và ngang?
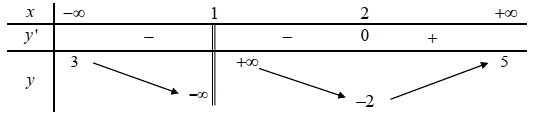
A. 3 .
B. 1.
C. 2.
D. 4.
Trả lời
Lời giải
Dựa vào bản biến thiên ta có:
\[\mathop {\lim }\limits_{x \to + \infty } y = 5;\,\mathop {\lim }\limits_{x \Rightarrow - \infty } y = 3\] nên suy ra đồ thị hàm số có hai đường tiệm cận ngang là \(y = 5;\,y = 3\)
Lại có: \(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty ;\,\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \) suy ra đồ thị hàm số có 1 đường tiệm cận đứng là \(x = 1\).
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận đứng và ngang.

