Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng ? A. ab < 0,bc > 0,cd < 0 B. ab < 0,bc < 0,cd > 0 C. ab > 0,bc > 0,cd < 0 D. ab >
43
27/04/2024
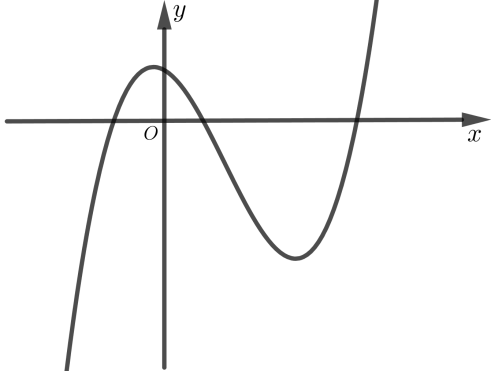
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng ?
A. \(ab < 0,bc > 0,cd < 0\)
B. \(ab < 0,bc < 0,cd > 0\)
C. \(ab > 0,bc > 0,cd < 0\)
D. \(ab > 0,bc > 0,cd > 0\)
Trả lời
Lời giải
Chọn A
Từ dáng điệu của đồ thị ta có ngay được:
\( \oplus \) \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \Rightarrow a > 0\).
\( \oplus \) Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên \(d > 0\).
Ta có: \(y' = 3a{x^2} + 2bx + c\)
Mặt khác dựa vào đồ thị ta thấy phương trình \(y' = 0\) có hai nghiệm trái dấu và tổng hai nghiệm này luôn dương nên \(\left\{ \begin{array}{l}ac < 0\\ - \frac{{2b}}{{3a}} > \end{array} \right. \Rightarrow \left\{ \begin{array}{l}c < 0\\b < 0\end{array} \right.\) (do \(a > 0\))
Do đó: \(ab < 0,bc > ,cd < 0\).
Vậy đáp án A.