Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị hàm số như hình bên. Khẳng định nào sau đây là đúng? A. a < 0, b > 0, c = 0, d > 0 B. a > 0, b < 0, c > 0, d > 0. C. a < 0, b < 0,
44
03/05/2024
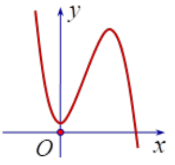
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị hàm số như hình bên. Khẳng định nào sau đây là đúng?
A. \(a < 0\), \(b > 0\), \(c = 0\), \(d > 0\).
B. \(a > 0\), \(b < 0\), \(c > 0\), \(d > 0\).
C. \(a < 0\), \(b < 0\), \(c = 0\), \(d > 0\).
D. \(a < 0\), \(b > 0\), \(c > 0\), \(d > 0\).
Trả lời
Lời giải
Chọn A
Tập xác định: \(D = \mathbb{R}\).
\(y' = 3a{x^2} + 2bx + c\).
Dựa vào đồ thị hàm số:
+) \(\mathop {lim}\limits_{x \to + \infty } y = - \infty \) nên \(a < 0\).
+) Giao điểm của đồ thị hàm số với trục tung là \(\left( {0;d} \right)\). Do đó \(d > 0\).
+) Gọi \({x_1}\), \({x_2}\) là hai điểm cực trị của hàm số.
Ta có: \({x_1} + {x_2} > 0 \Leftrightarrow \frac{{ - 2b}}{{3a}} > 0 \Leftrightarrow - 2b\left\langle {0 \Leftrightarrow b} \right\rangle 0\) (vì \(a < 0\)).
\({x_1}.{x_2} = 0 \Leftrightarrow \frac{c}{{3a}} = 0 \Leftrightarrow c = 0\).
Vậy \(a < 0\), \(b > 0\), \(c = 0\), \(d > 0\).