Cho hàm số f(x), có bảng biến thiên của hàm số f'(x) như sau: Số cực trị của hàm số y = f(x^2 + 2x) là A. 5 B. 4 C. 3 D. 7
53
25/04/2024
Cho hàm số \(f(x)\), có bảng biến thiên của hàm số \(f'(x)\) như sau:

Số cực trị của hàm số \(y = f({x^2} + 2x)\) là
A. \(5\).
B. \(4\).
C. \(3\).
D. \(7\).
Trả lời
Lời giải
Chọn D
Ta có \(y' = \left( {2x + 2} \right)f'({x^2} + 2x)\)
Khi đó, \(y' = 0 \Leftrightarrow \left( {2x + 2} \right)f'({x^2} + 2x) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\f'({x^2} + 2x) = 0\end{array} \right.\)
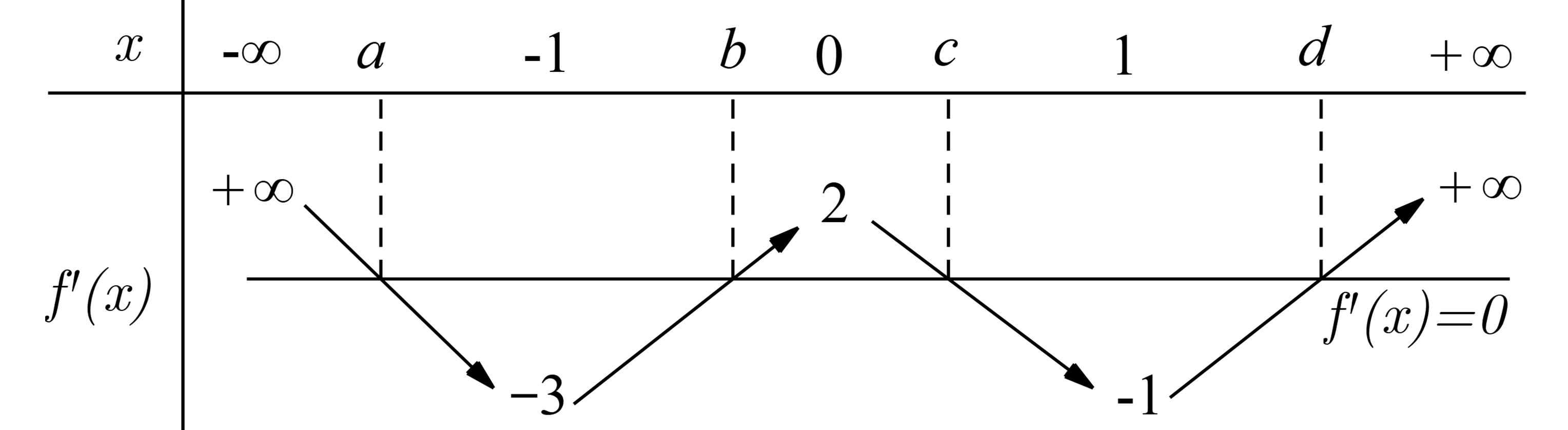
Dựa vào bảng biến thiên của hàm số \(f'(x)\), ta có: \(f'({x^2} + 2x) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x = a\,(a < - 1)\,\,\,\,\,\,\,\,\,(1)\\{x^2} + 2x = b\,( - 1 < b < 0)\,(2)\\{x^2} + 2x = c\,\,(0 < c < 1)\,\,\,\,\,(3)\\{x^2} + 2x = d\,\,(d > 1)\,\,\,\,\,\,\,\,\,\,\,\,(4)\end{array} \right.\)
Lập BBT của hàm số \(g(x) = {x^2} + 2x\), từ đó ta suy ra được:
+) Phương trình (1) vô nghiệm
+) Phương trình (2) có 2 nghiệm âm phân biệt \({x_1}\), \({x_2}\) và \({x_1} < - 1 < {x_2}\)
+) Phương trình (3) có 2 nghiệm trái dấu \({x_3}\), \({x_4}\) và \({x_3} < {x_1} < - 1 < {x_2} < {x_4}\).
+) Phương trình (4) có 2 nghiệm trái dấu \({x_5}\), \({x_6}\) và \({x_5} < {x_3} < {x_1} < - 1 < {x_2} < {x_4} < {x_6}\).
Ta có bảng xét dấu \(y'\) như sau:

Suy ra hàm số \(y = f({x^2} + 2x)\) có 7 điểm cực trị.



