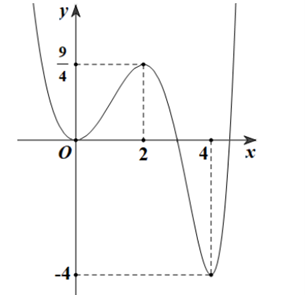
Cho hàm số f( x ) có đạo hàm liên tục trên R. Đồ thị của hàm số y = f( 5 - 2x) như hình vẽ sau. Có bao nhiêu giá trị thực của tham số m thuộc
45
27/04/2024
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f\left( {5 - 2x} \right)\) như hình vẽ sau. Có bao nhiêu giá trị thực của tham số \(m\)thuộc khoảng \(\left( { - 9;9} \right)\) thỏa mãn \(2m \in \mathbb{Z}\) và hàm số \(y = \left| {2f\left( {4{x^3} + 1} \right) + m - \frac{1}{2}} \right|\) có 5 điểm cực trị?
A. \[26\].
B. \[25\].
C. \[27\].
D. \[24\].
Trả lời
Lời giải
Ta có \(y = f\left( {5 - 2x} \right) \Rightarrow y' = - 2f'\left( {5 - 2x} \right)\). Từ đồ thị, suy ra
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = 4\end{array} \right.\). Đặt \[t = 5 - 2x \Rightarrow x = \frac{{5 - t}}{2} \Rightarrow f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 5\\t = 1\\t = - 3\end{array} \right.\]
Đặt \[g\left( x \right) = 2f\left( {4{x^3} + 1} \right) + m - \frac{1}{2} \Rightarrow g'\left( x \right) = 24{x^2}f'\left( {4{x^3} + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\4{x^3} + 1 = 5 \Rightarrow {x^3} = 1\\4{x^3} + 1 = 1 \Rightarrow {x^3} = 0\\4{x^3} + 1 = - 3 \Rightarrow {x^3} = - 1\end{array} \right.\]
Từ đó suy ra \[g\left( x \right)\] có 3 cực trị. Để \[y = \left| {g\left( x \right)} \right|\] có 5 cực trị thì phương trình \[g\left( x \right) = 0 \Leftrightarrow f\left( {4{x^3} + 1} \right) = \frac{{1 - 2m}}{4}\] có 2 nghiệm đơn phân biệt.
Đặt \[u = 4{x^3} + 1 \Rightarrow x = \sqrt[3]{{\frac{{u - 1}}{4}}}\] và phương trình trở thành: \[f\left( u \right) = \frac{{1 - 2m}}{4}\].
Từ đây, kết hợp với đồ thị ta có điều kiện là \[\left[ \begin{array}{l}\frac{{1 - 2m}}{4} \ge \frac{9}{4}\\ - 4 < \frac{{1 - 2m}}{4} \le 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}2m \le - 8\\1 \le 2m < 17\end{array} \right.\].
Do \[m \in \left( { - 9\,;\,9} \right),\,2m \in \mathbb{Z} \Rightarrow \left[ \begin{array}{l}2m \in \left\{ { - 17, - 16, \ldots , - 9, - 8} \right\}\\2m \in \left\{ {1,2,3, \ldots ,16} \right\}\end{array} \right.\].
Vậy có tất cả 26 giá trị của \[m\]thỏa mãn yêu cầu bài toán.