Cho hàm số f( x ) có bảng biến thiên như sau: Biết f( 0 ) = 0, số nghiệm thuộc đoạn [ -pi /6; pi /3] của phương trình
36
27/04/2024
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
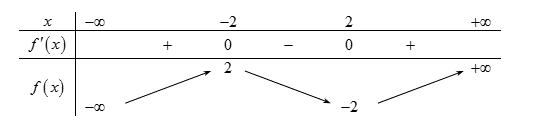
Biết \(f\left( 0 \right) = 0\), số nghiệm thuộc đoạn \(\left[ { - \frac{\pi }{6};\frac{{7\pi }}{3}} \right]\) của phương trình \(f\left( {f\left( {\sqrt 3 \sin x + \cos x} \right)} \right) = 1\) là
A. \(5\).
B. \(3\).
C. \(4\).
D. \(2\).
Trả lời
Lời giải
* Xét \(g(x) = f\left( {f\left( {\sqrt 3 \sin x + \cos x} \right)} \right)\) với \(x \in \left[ { - \frac{\pi }{6};\frac{{7\pi }}{3}} \right]\)
* Đặt \(u(x) = \sqrt 3 \sin x + \cos x = 2\cos \left( {x - \frac{\pi }{3}} \right)\)
\( \Rightarrow \,\,\,u'(x) = - 2\sin \left( {x - \frac{\pi }{3}} \right)\); \(u'(x) = 0\,\,\,\, \Rightarrow \,\,\,x \in \left\{ {\frac{\pi }{3},\,\frac{{4\pi }}{3},\,\frac{{7\pi }}{3}} \right\}\)
* Đặt \(v(x) = f\left[ {u(x)} \right]\) \( \Rightarrow \,\,\,v'(x) = u'(x).f'\left[ {u(x)} \right]\)
\(g(x) = f\left( {v(x)} \right)\) \( \Rightarrow \,\,\,g'(x) = v'(x).f'\left[ {v(x)} \right]\)

