Cho đường tròn (O;R) với dây AB < 2R cố định Gọi C là điểm thuộc cung lớn AB sao cho nhọn ,Mvà N lần lược là điểm chính giữa cung nhỏ AB và cung nhỏ AC. Gọi I là giao của BN và CM. Dây MN cắ
91
07/05/2024
Cho đường tròn (O;R) với dây AB < 2R cố định Gọi C là điểm thuộc cung lớn AB sao cho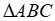 
nhọn ,Mvà N lần lược là điểm chính giữa cung nhỏ AB và cung nhỏ AC. Gọi I là giao của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K. Chứng minh rằng :
1) Tứ giác BMHI nội tiếp.
2) NI.NB = NH.NM
3) KH là phân giác củ góc AKI, IA là phân giác của góc KIH
4) Khi điểm C di động trên cung lớn AB và thỏa mãn điều kiện đề bài thì tổng hai bán kính của hai đường tròn ngoại tiếp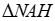 
và 
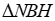có giá trị không đổi .
Trả lời
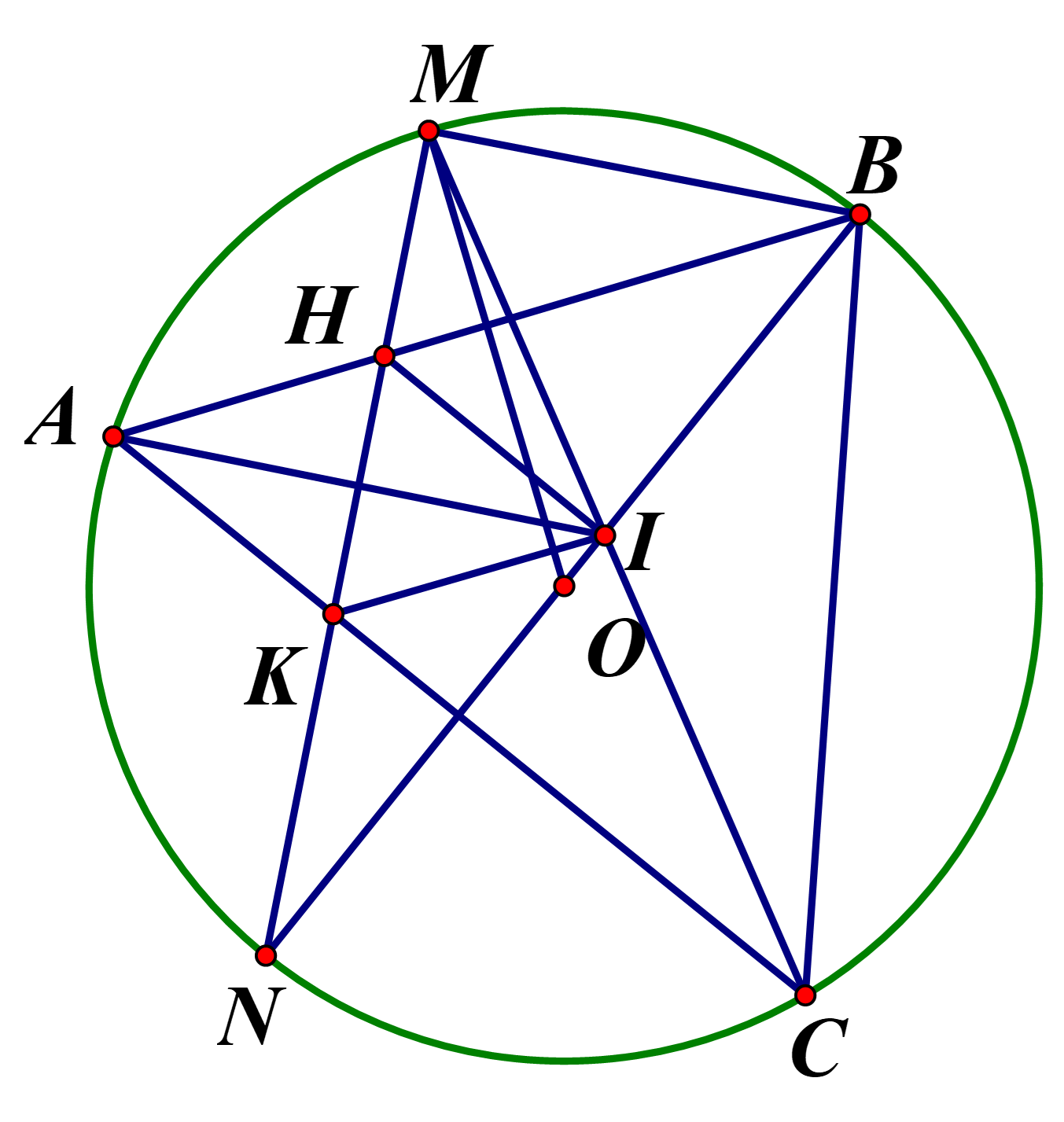
1) Ta có: \(AN = NC \Rightarrow \angle ABN = \angle NMC \Rightarrow BMHI\)là tứ giác nội tiếp
2) Theo câu a, tứ giác \(BMHI\)nội tiếp
\( \Rightarrow \angle HMB + \angle HIB = 180^\circ \)mà \(\angle NIH + \angle HIB = 180^\circ \Rightarrow \angle HNB = \angle HIB\)
Xét \(\Delta NIH\)và \(\Delta NMB\)có: \(\angle MNB\)chung,
\( \Rightarrow \frac{{NI}}{{NM}} = \frac{{NH}}{{NB}} \Rightarrow NI.NB = NM.NH\)
3) Ta có: \(MA = MB \Rightarrow \angle ACM = \angle MNB \Rightarrow KINC\)là tứ giác nội tiếp
\( \Rightarrow \angle KIN = \angle KCN\)(cùng chắn mà \(\angle KCN = \angle ABN\)(cùng chắn
\( \Rightarrow \angle KIN = \angle ABN\), mà chúng đồng vi \( \Rightarrow KI//AH\left( 1 \right)\)
Theo câu 1, tứ giác \(BHMI\)nội tiếp \( \Rightarrow \angle IMB = \angle IHB\)(cùng chắn
Mà \(\angle IMB = \angle CAB\), mà chúng đồng vị \( \Rightarrow IH//AK\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow AHIK\)là hình bình hành
Lại có :
\( \Rightarrow \angle AKH = \angle AHK \Rightarrow \Delta AHK\)cân tại A\( \Rightarrow AH = AK\)
Hình bình hành \(AHIK\)có \(AN = AK \Rightarrow AHIK\)là hình thoi\( \Rightarrow KH\)là đường phân giác \(\angle AKI \Rightarrow IA\)là phân giác \(\angle KIH\)
4) Gọi \({O_1},{O_2}\)lần lượt là tâm đường tròn ngoại tiếp \(\Delta ANH\)và \(\Delta BNH\)
\( \Rightarrow \Delta {O_1}AH\)cân tại \({O_1}\)và \(\Delta {O_2}BH\)cân tại \({O_2}\), có \(\angle A{O_1}H = 2\angle ANH\), \(\angle B{O_2}H = 2\angle BNH\)\( \Rightarrow \angle {A_1}OH = \angle B{O_2}H\)mà \(\angle ANH = \angle BNH\)
\( \Rightarrow \angle {O_1}AH = \angle {O_1}HA = \angle {O_2}HB = \angle O_2^{}BH\)
Gọi D là giao điểm của \(A{O_1}\)và \(B{O_2}\)có:
\(\Delta ADB\)cân tại \(D \Rightarrow M,O,D\)thẳng hàng
Có \(\angle AMD = \angle MAB = \angle ANM \Rightarrow MA\)là tiếp tuyến của \(\left( {{O_1}} \right) \Rightarrow \angle MAD = 90^\circ \)\( \Rightarrow MD\)là đường kính của \(\left( O \right) \Rightarrow D\)cố định
Ta chứng minh được : \(\angle A{O_1}H = \angle ADB \Rightarrow H{O_1}//D{O_2}\)
\( \Rightarrow \angle AOB = \angle H{O_2}B \Rightarrow H{O_2}//D{O_1}\)
Tứ giác \(H{O_1}D{O_2}\)là hình bình hành\( \Rightarrow {O_2}H = D{O_1}\)
Có \({R_1} + {R_2} = {O_1}A + {O_2}H = {O_1}A + {O_1}D = AD\)
\(A,D\)cố định \( \Rightarrow AD\)không đổi \( \Rightarrow {R_1} + {R_2}\)không đổi
