Cho đường tròn (C) x^2 + y^2 -4x-6y+5 =0 . Đường thẳng d đi qua A (3;2) và cắt (C) theo một dây

C. $x-y-1=0$.

Trả lời

$\begin{array}{l}f(x;y)=x^2+y^2-4x-6y+5.\\ f(3;2)=9+4-12-12+5=-6<0.\end{array}$

Vậy A ( 3;2)  ở trong (C)

.

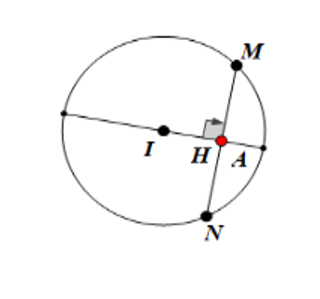
Dựa vào ảnh trên ta thấy dây cung MN ngắn nhất $\iff IH$ lớn nhất $\iff H\equiv A\iff MN$ có vectơ pháp tuyến là $\overrightarrow{IA}=(1;-1)$. Vậy d có phương trình:

$1(x-3)-1(y-2)=0\iff x-y-1=0.$