Cho các biểu thức A = 1 - căn bậc hai của x/ 1 + căn bậc hai của x và với 1)Tính giá trị của biểu thức A khi 2)Rút gọn B 3) Tìm a để phương trình A - B = a có nghiệm.
40
07/05/2024
Cho các biểu thức
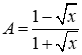 và
và 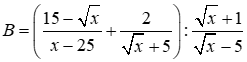 với
với 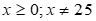
1)Tính giá trị của biểu thức A khi 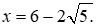
2)Rút gọn B
3) Tìm a để phương trình A - B = a có nghiệm.
Trả lời
1) Ta có \(x = 6 - 2\sqrt 5 \Rightarrow \sqrt x = \sqrt 5 - 1 \Rightarrow A = \frac{{1 - \left( {\sqrt 5 - 1} \right)}}{{1 + \left( {\sqrt 5 - 1} \right)}} = \frac{{2 - \sqrt 5 }}{{\sqrt 5 }}\)
\(\begin{array}{l}2)B = \left[ {\frac{{15 - \sqrt x }}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 5} \right)}} + \frac{{2\left( {\sqrt x - 5} \right)}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 5} \right)}}} \right].\frac{{\sqrt x - 5}}{{\sqrt x + 1}}\\ = \frac{{\sqrt x + 5}}{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 5} \right)}}.\frac{{\sqrt x - 5}}{{\sqrt x + 1}} = \frac{1}{{\sqrt x + 1}}\left( \begin{array}{l}x \ge 0\\x \ne 25\end{array} \right)\end{array}\)
3) Với \(x \ge 0,x \ne 25\)
\(\begin{array}{l} \Rightarrow A - B = a \Leftrightarrow \frac{{1 - \sqrt x }}{{1 + \sqrt x }} - \frac{1}{{\sqrt x + 1}} = a \Leftrightarrow \frac{{ - \sqrt x }}{{1 + \sqrt x }} = a\\ \Rightarrow - \sqrt x = a\left( {1 + \sqrt x } \right) \Leftrightarrow \left( {a + 1} \right)\sqrt x = - a\end{array}\)
TH1: \(a = - 1\):Vô nghiệm
\(TH2:a \ne - 1\). Phương trình có dạng \(\sqrt x = \frac{{ - a}}{{a + 1}}\)
Phương trình này có nghiệm thỏa \(x \ge 0,x \ne 25\)
\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - a}}{{a + 1}} \ge 0\\\frac{{ - a}}{{a + 1}} \ne 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 \le a \le 0\\6a \ne - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne \frac{{ - 5}}{6}\\ - 1 \le a \le 0\end{array} \right.\)
Do \(a \ne - 1\)nên giá trị cần tìm của \(a:\left\{ \begin{array}{l} - 1 < a \le 0\\a \ne \frac{{ - 5}}{6}\end{array} \right.\)
Do \(a \ne - 1\)nên giá trị cần tìm của \(a:\left\{ \begin{array}{l} - 1 < a \le 0\\a \ne - \frac{5}{6}\end{array} \right.\)
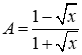 và
và 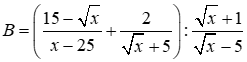 với
với ![]()
![]()
