Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?
A. 0.
B. 1.
C. 2.
D. 3.
Đáp án đúng là: D
Gọi (O1), (O2), (O3) là ba đường tròn thỏa mãn yêu cầu bài toán.
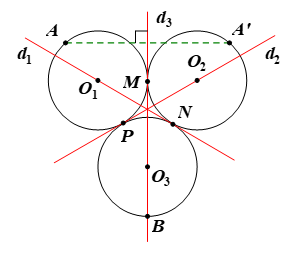
Gọi M, N, P lần lượt là tiếp điểm của các cặp đường tròn (O1) và (O2); (O2) và (O3); (O1) và (O3) (hình vẽ).
Chọn các đường thẳng d1, d2, d3 lần lượt là các đường thẳng đi qua các cặp điểm O1 và N; O2 và P; O3 và M.
Lấy điểm A nằm trên hình ℋ nhưng không nằm trên đường thẳng d3.
Ta đặt A’ là ảnh của A qua phép đối xứng trục d3.
Khi đó A’ nằm trên hình ℋ ban đầu.
Lấy điểm B nằm trên hình ℋ và nằm trên đường thẳng d3.
Ta thấy B là ảnh của chính nó qua phép đối xứng trục d3.
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình ℋ, ta cũng xác định được ảnh của điểm đó qua phép đối xứng trục d3 trên hình ℋ.
Do đó phép đối xứng trục d3 biến hình ℋ thành chính nó.
Vì vậy d3 là trục đối xứng của hình ℋ.
Chứng minh tương tự với hai đường thẳng d1, d2, ta được d1, d2 cũng là trục đối xứng của hình ℋ.
Vậy hình ℋ có 3 trục đối xứng là các đường thẳng d1, d2, d3.
Do đó ta chọn phương án D.