Biết rằng G là đồ thị có 6 đỉnh, 8 cạnh và các đỉnh của nó có bậc 2 hoặc 4. Đồ thị có bao nhiêu đỉnh bậc 4? Hãy vẽ một đồ thị như vậy.

Theo Định lí, ta có tổng tất cả các bậc của các đỉnh bằng hai lần số cạnh của đồ thị.

Suy ra tổng tất cả các bậc của các đỉnh là: 2.8 = 16.

Theo đề, ta có đồ thị G có 6 đỉnh và các đỉnh của đồ thị G có bậc 2 hoặc 4.

Mà 2 + 2 + 2 + 2 + 4 + 4 = 16.

Vậy đồ thị G có 2 đỉnh bậc 4 và 4 đỉnh bậc 2.

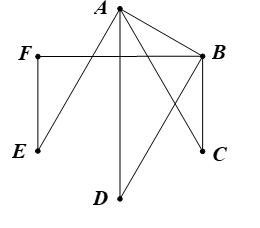
Ta vẽ đồ thị như sau:

– Gọi 6 đỉnh của đồ thị là A, B, C, D, E, F có bậc của mỗi đỉnh lần lượt là 4; 4; 2; 2; 2; 2.

– Do có hai đỉnh A, B có số bậc cao nhất là 4 nên ta tùy ý chọn một đỉnh là đỉnh A để bắt đầu vẽ. Xuất phát từ đỉnh A, ta lần lượt nối tới các đỉnh B, C, D, E, mỗi đỉnh một cạnh.

– Tiếp theo, ta vẽ từ đỉnh có số bậc cao nhất còn lại là đỉnh B. Do từ đỉnh B đã có sẵn một cạnh đã vẽ ở trên nên xuất phát từ đỉnh B, ta lần lượt vẽ thêm đến các đỉnh C, D, F, mỗi đỉnh một cạnh.

– Cuối cùng, ta thấy các đỉnh C, D đều có số bậc là 2. Mà hai đỉnh này ta đã vẽ xong hai cạnh cho mỗi đỉnh nên kế tiếp ta sẽ xét đến hai điểm còn lại là E, F.

Ta thấy với các đỉnh E, F, mỗi đỉnh đều đã có sẵn một cạnh đã vẽ trước đó nên ta nối một cạnh giữa hai đỉnh E và F.

Một đồ thị thỏa mãn yêu cầu bài toán là:

Chú ý: Ngoài đồ thị đã vẽ ở trên, ta có thể vẽ thêm các đồ thị khác cũng thỏa mãn yêu cầu đề bài.