Bạn Minh muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều ABC có cạnh bằng 90cm. Bạn muốn cắt mảnh tôn hình chữ nhật MNPQ từ mảnh tôn nguyên liệu (với
37
03/05/2024
Bạn Minh muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều \[ABC\] có cạnh bằng \[90{\rm{ }}\left( {{\rm{cm}}} \right)\]. Bạn muốn cắt mảnh tôn hình chữ nhật \[MNPQ\] từ mảnh tôn nguyên liệu (với \[M\], \[N\] thuộc cạnh \[BC\]; \[P\], \[Q\] tương ứng thuộc cạnh \[AC\] và \[AB\]) để tạo thành hình trụ có chiều cao bằng \[MQ\]. Thể tích lớn nhất của chiếc thùng mà bạn Minh có thể làm được là
A. \(\frac{{91125}}{{4\pi }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
B. \(\frac{{91125}}{{2\pi }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
C. \[\frac{{13500.\sqrt 3 }}{\pi }\left( {{\rm{c}}{{\rm{m}}^3}} \right)\]
D. \(\frac{{108000\sqrt 3 }}{\pi }\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Trả lời
Lời giải
Chọn C
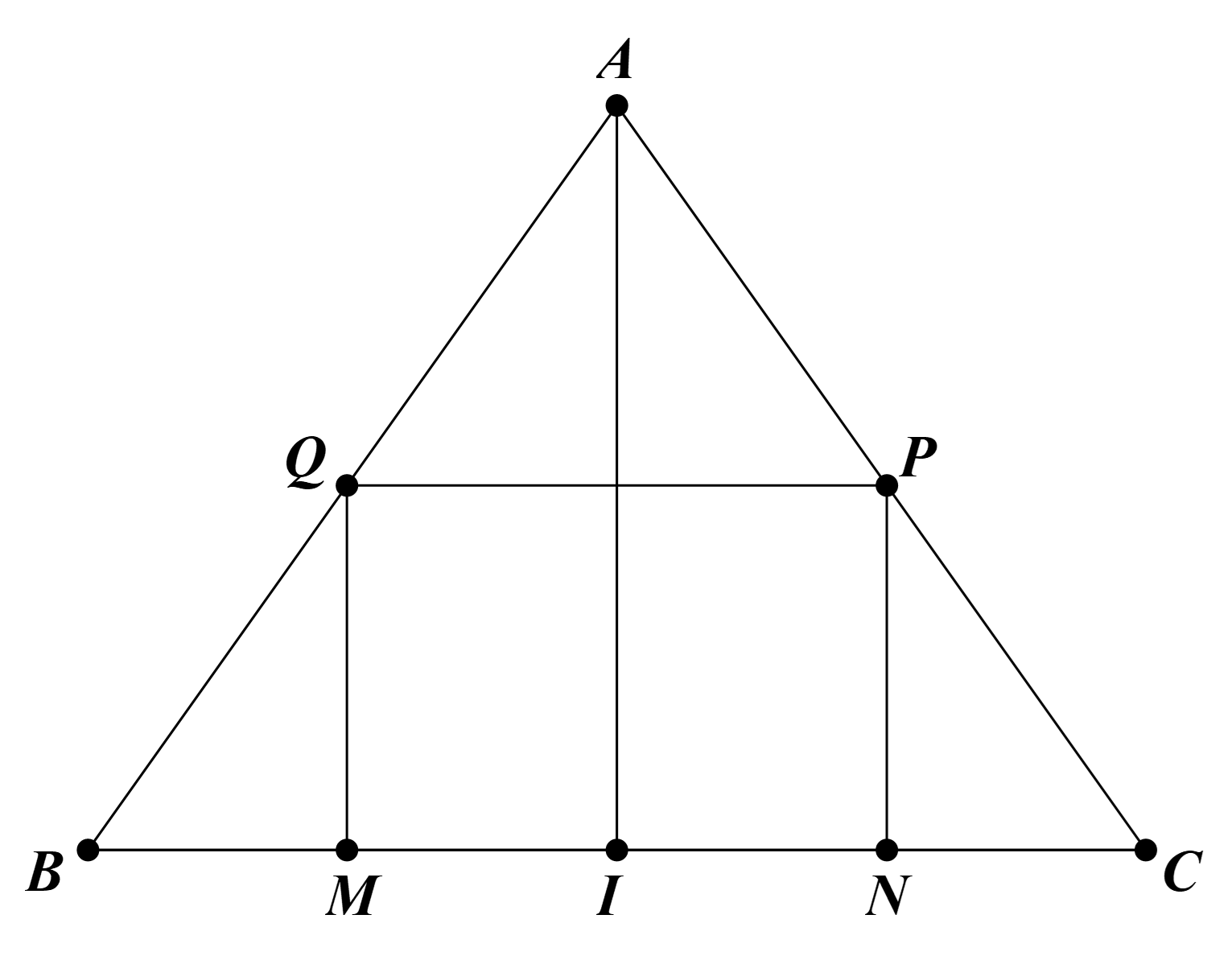
Gọi \[I\] là trung điểm \[BC\]. Suy ra \[I\] là trung điểm \[MN\]. Đặt \[MN = x\], \[\left( {0 < x < 90} \right)\].
Ta có: \(\frac{{MQ}}{{AI}} = \frac{{BM}}{{BI}}\)\( \Leftrightarrow MQ = \frac{{\sqrt 3 }}{2}\left( {90 - x} \right)\); gọi \(R\) là bán kính của trụ \( \Rightarrow R = \frac{x}{{2\pi }}\).
Thể tích của khối trụ là: \({V_T} = \pi {\left( {\frac{x}{{2\pi }}} \right)^2}\frac{{\sqrt 3 }}{2}\left( {90 - x} \right) = \frac{{\sqrt 3 }}{{8\pi }}\left( { - {x^3} + 90{x^2}} \right)\)
Xét \(f\left( x \right) = \frac{{\sqrt 3 }}{{8\pi }}\left( { - {x^3} + 90{x^2}} \right)\) với \(0 < x < 90\), \(f'\left( x \right) = \frac{{\sqrt 3 }}{{8\pi }}\left( { - 3{x^2} + 180x} \right)\), \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 60}\end{array}} \right.\).
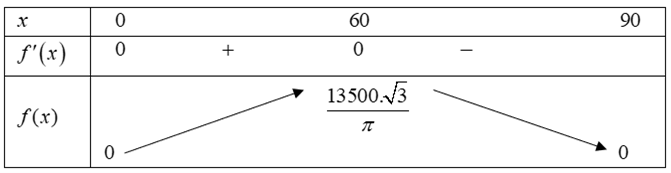
Khi đó suy ra \[\mathop {\max }\limits_{x \in (0;90)} f\left( x \right) = f\left( {60} \right) = \frac{{13500.\sqrt 3 }}{\pi }\].
