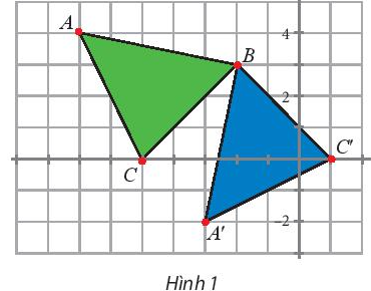
a) Để tìm phép biến hình biến ∆BAC thành ∆BA’C’, ta tìm phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’, biến điểm C thành điểm C’.
Với A(–7; 4), B(–2; 3), C(–5; 0), A’(–3; –2), C’(1; 0), ta có:
.
Suy ra và .
Khi đó .
Vì vậy .
Suy ra phép biến hình biến đoạn thẳng BA thành đoạn thẳng BA’ là phép biến hình biến điểm B thành điểm B, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác (BA, BA’) = 90° (1)
Thực hiện tương tự, ta được và .
Suy ra phép biến hình biến đoạn thẳng BC thành đoạn thẳng BC’ là phép biến hình biến điểm B thành điểm B, biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác (BC, BC’) = 90° (2)
Từ (1), (2), ta thu được phép biến hình biến ∆BAC thành ∆BA’C’ là phép biến hình biến điểm B thành chính nó, biến điểm A thành điểm A’ sao cho BA’ = BA và góc lượng giác (BA, BA’) = 90° và biến điểm C thành điểm C’ sao cho BC’ = BC và góc lượng giác (BC, BC’) = 90°.
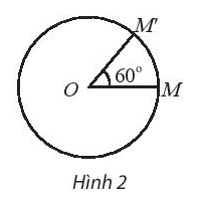
b) Đặt f(M) = M’. Trong đó, M’ là điểm nằm trên (C) sao cho góc lượng giác (OM, OM’) bằng 60°.
Ta thấy f là một quy tắc sao cho ứng với mỗi điểm M đều xác định duy nhất một điểm M’.
Vậy f là một phép biến hình.
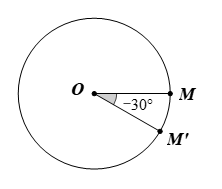
Cách vẽ điểm M’ theo quy tắc trên với góc lượng giác (OM, OM’) bằng –30°:
– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.
– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng –30°.
Ta có hình vẽ sau: