1) Giải hệ phương trình sau 2) Cho Parabol và đường thẳng (d): y = 2x + 3 a) Chứng minh rằng đường thẳng d cắt parabol (P) tại hai điểm phân biệt A, B và tìm tọa độ của A, B b)
54
07/05/2024
1) Giải hệ phương trình sau 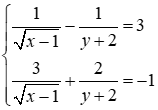
2) Cho Parabol 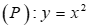 và đường thẳng (d): y = 2x + 3
và đường thẳng (d): y = 2x + 3
a) Chứng minh rằng đường thẳng d cắt parabol (P) tại hai điểm phân biệt A, B và tìm tọa độ của A, B
b) Xác định điểm C thuộc cung nhỏ AB của parabol (P) sao cho diện tích 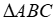 lớn nhất .
lớn nhất .
Trả lời
\(1)\left\{ \begin{array}{l}\frac{1}{{\sqrt {x - 1} }} - \frac{1}{{y + 2}} = 3\\\frac{3}{{\sqrt {x - 1} }} + \frac{2}{{y + 2}} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 1} = 1\\y + 2 = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - \frac{5}{2}\end{array} \right.\)
2) Phương trình hoành độ giao điểm \(\left( P \right),\left( d \right):\)
\({x^2} - 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_A} = 3 \Rightarrow A\left( {3;9} \right)\\{x_B} = - 1 \Rightarrow B\left( { - 1;1} \right)\end{array} \right.\)
b) \(C\left( {x;{x^2}} \right)\)và \(A',B',C'\)lần lượt là chân đường cao hạ xuống \(Ox\)
\(\begin{array}{l}{S_{ABC}} = {S_{AA'B'B}} + {S_{ACC'A'}} - {S_{BCC'B'}} = 2{x^2} + 4x + 6 = 8 - 2{\left( {x - 1} \right)^2} \le 8\\ \Rightarrow MaxS = 8 \Leftrightarrow C\left( {1;1} \right)\end{array}\)
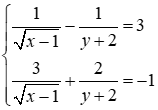
![]() và đường thẳng (d): y = 2x + 3
và đường thẳng (d): y = 2x + 3![]() lớn nhất .
lớn nhất .