Bài tập tính góc ngoài của tam giác

1. Phương pháp giải

- Định nghĩa: Góc ngoài của một tam giác là góc kề bù với một góc của tam giác ấy.

Cho tam giác ABC, vẽ tia đối CD của tia CB, khi đó $\widehat{ACD}$ là góc ngoài tại đỉnh C của tam giác ABC.

- Tính chất

+ Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.

Ta có: ${\widehat{A}}_1;{\widehat{B}}_1;{\widehat{C}}_1$ lần lượt là các góc ngoài tại các đỉnh A; B; C của tam giác ABC.

Khi đó:

$\widehat{A_1}=\widehat{B_2}+\widehat{C_2}$

$\widehat{B_1}=\widehat{A_2}+\widehat{C_2}$

$\widehat{C_1}=\widehat{B_2}+\widehat{A_2}$

- Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó:

${\widehat{A}}_1>{\widehat{B}}_2;{\widehat{A}}_1>{\widehat{C}}_2$(Hình trên)

2. Ví dụ minh họa

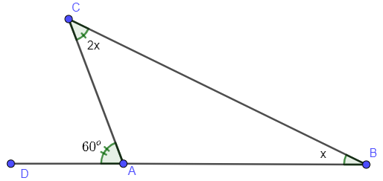
Ví dụ 1: Tính số đo x trong hình vẽ sau

Lời giải:

Xét tam gác ABC có góc $\widehat{CAD}$ là góc ngoài tại đỉnh A của tam giác ABC.

Ta có:

$\widehat{CAD}=\widehat{ACB}+\widehat{CBA}$ (định lý góc ngoài của tam giác)

Mà $\widehat{CAD}=60°$; $\widehat{ACB}=2x$; $\widehat{ABC}=x$ thay vào ta có:

$60°=2x+x$

$3x=60°$

$x=60°:3$

$x=20°$

Vậy $x=20°$.

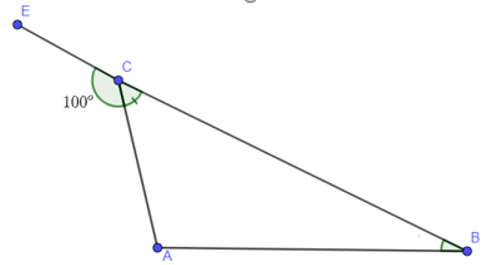
Ví dụ 2: Cho tam giác ABC góc ngoài tại đỉnh C có số đo bằng $100°$, $3\widehat{A}=2\widehat{B}$.

Tính số đo góc $\widehat{B};\widehat{C}$.

Lời giải:

Trên tia đối của tia CB, vẽ tia CE

Ta có: Góc ngoài tại đỉnh C của tam giác ABC là góc $\widehat{ECA}=100°$

Vì $\widehat{ECA}$ và $\widehat{BCA}$ là hai góc kề bù nên:

$\widehat{ECA}+\widehat{BCA}=180°$

Thay $\widehat{ECA}=100°$ và ta có:

$100°+\widehat{BCA}=180°$

$\Rightarrow \widehat{BCA}=180°-100°$

$\Rightarrow \widehat{BCA}=80°$

Xét tam giác ABC ta có:

$\widehat{A}+\widehat{B}=\widehat{ECA}$ (tính chất góc ngoài tam giác)

$\widehat{A}+\widehat{B}=100°$   (1)

Mà $3\widehat{A}=2\widehat{B}\Rightarrow \widehat{A}=\frac{2\widehat{B}}{3}$ thay vào (1) ta có:

$\frac{2\widehat{B}}{3}+\widehat{B}=100°$

$\left(\frac{2}{3}+1\right)\widehat{B}=100°$

$\frac{5}{3}\widehat{B}=100°$

$\widehat{B}=100°:\frac{5}{3}$

$\widehat{B}=60°$

Vậy góc $\widehat{B}=60°$; $\widehat{ACB}=80°$.

3. Bài tập vận dụng

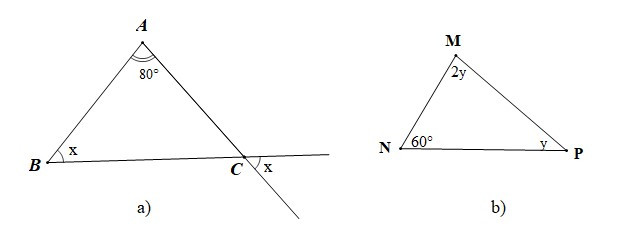
Bài 1. Tìm số đo góc x và y trong mỗi hình vẽ sau:

Hướng dẫn giải:

• Hình a)

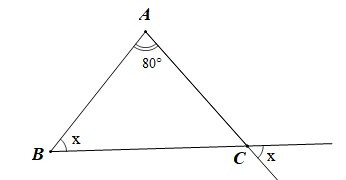
Ta có $\widehat{\mathrm{ACB}}=\mathrm{x}$ (hai góc đối đỉnh), $\widehat{\mathrm{B}}=\mathrm{x}$ (giả thiết)

Nên $\widehat{\mathrm{B}}=\widehat{\mathrm{ACB}}=\mathrm{x}.$

Xét DABC có $\widehat{\mathrm{A}}+\widehat{\mathrm{B}}+\widehat{\mathrm{ACB}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{B}}+\widehat{\mathrm{ACB}}=180°-\widehat{\mathrm{A}}$

Mà $\widehat{\mathrm{A}}=80°,\widehat{\mathrm{B}}=\widehat{\mathrm{ACB}}=\mathrm{x}$ 

Nên x + x = 180° – 80°

Hay 2x = 100°

Do đó x = 50°

Vậy x = 50°.

• Hình b)

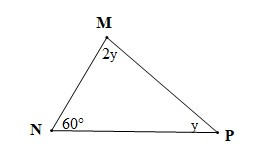
Xét DMNP có: $\widehat{\mathrm{M}}+\widehat{\mathrm{N}}+\widehat{\mathrm{P}}=180°$ (tổng ba góc trong một tam giác)

Hay y + 2y + 60° =180°

Suy ra 3y = 180° – 60°

3y = 120°

y = 120° : 3 = 40°

Vậy y = 40°.

Bài 2. Tìm số đo góc ABC trong hình vẽ sau, biết Ax // Cy

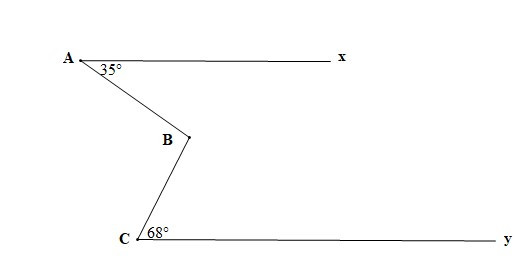
Hướng dẫn giải

Gọi giao điểm của AB và đường thẳng Cy là D, ta có hình vẽ:

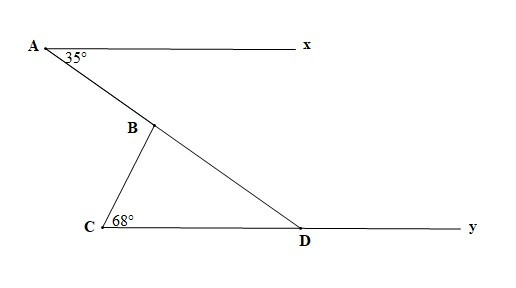
Vì Ax // Cy (giả thiết) nên $\widehat{\mathrm{xAD}}=\widehat{\mathrm{A}\text{D}\mathrm{C}}$ (hai góc so le trong)

Mà $\widehat{\mathrm{xAD}}=35°$ nên $\widehat{\mathrm{A}\text{D}\mathrm{C}}=35°$

Vì $\widehat{\mathrm{ABC}}$ là góc ngoài của tam giác BCD tại đỉnh B

Nên $\widehat{\mathrm{ABC}}=\widehat{\mathrm{BC}\text{D}}+\widehat{\mathrm{BDC}}$ (tính chất góc ngoài của một tam giác)

Suy ra $\widehat{\mathrm{ABC}}=68°+35°=103°$

Vậy số đo góc ABC là 103°.

Bài 3. Cho tam giác ABC vuông tại A có $\widehat{\mathrm{C}}=30°.$ Lấy điểm D nằm trên cạnh AC sao cho $\widehat{\mathrm{CBD}}=20°.$ Tính số đo của:

a) $\widehat{\mathrm{ADB}};$

b) $\widehat{\mathrm{ABD}}.$

Hướng dẫn giải

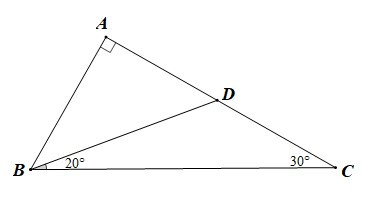
a) Xét DBCD có $\widehat{\mathrm{ADB}}$ là góc ngoài của tam giác tại đỉnh D

Do đó $\widehat{\mathrm{ADB}}=\widehat{\mathrm{C}}+\widehat{\mathrm{CBD}}$ (tính chất góc ngoài của tam giác)

Suy ra $\widehat{\mathrm{ADB}}=30°+20°=50°.$

Vậy $\widehat{\mathrm{ADB}}=50°.$

b) Tam giác ABC vuông tại A nên $\widehat{\mathrm{A}}=90°$

Do đó tam giác ABD vuông tại A.

Khi đó $\widehat{\mathrm{ABD}}+\widehat{\mathrm{ADB}}=90°$ (tổng hai góc nhọn trong tam giác vuông bằng 90°)

Suy ra $\widehat{\mathrm{ABD}}=90°-\widehat{\mathrm{ADB}}$

Do đó $\widehat{\mathrm{ABD}}=90°-50°=40°.$

Vậy $\widehat{\mathrm{ABD}}=40°.$

Câu 4. Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:

A. 55°;

B. 44°;

C. 33°;

D. 22°.

Hướng dẫn giải

Đáp án đúng là: C

Ta vẽ tam giác ABC vuông tại A có $\widehat{\mathrm{B}}=57°$ để mô tả hình ảnh chiếc thang dựa vào tường như đề bài.

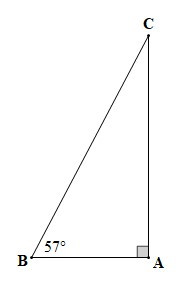
Trong tam giác ABC vuông tại A ta có: $\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{\mathrm{C}}=90°-\widehat{\mathrm{B}}=90°-57°=33°$ 

Vậy độ nghiêng của chiếc thang so với bức tường là 33°.

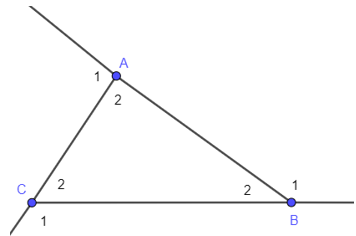
Câu 2. Cho hình vẽ sau:

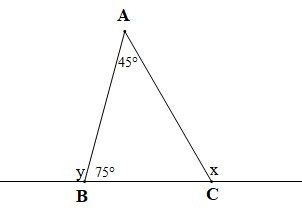
Số đo x, y lần lượt là:

A. 105° và 120°;

B. 120° và 105°;

C. 102° và 150°;

D. 150° và 102°.

Hướng dẫn giải

Đáp án đúng là: B

Tam giác ABC có góc x là góc ngoài của tam giác tại đỉnh C

Nên $\mathrm{x}=\widehat{\mathrm{A}}+\widehat{\mathrm{ABC}}$ (tính chất góc ngoài của tam giác)

Do đó x = 45° + 75° = 120°

Ta có: $\mathrm{y}+\widehat{\mathrm{ABC}}=180°$ (hai góc kề bù)

Suy ra $\mathrm{y}=180°-\widehat{\mathrm{ABC}}=180°-75°=105°$

Vậy số đo góc x, y lần lượt là 120° và 105°.

Câu 6. Cho hình vẽ biết $\widehat{\mathrm{ABC}}=50°,\widehat{\mathrm{ACB}}=40°$ và $\widehat{\mathrm{BAE}}=\widehat{\mathrm{AED}}.$

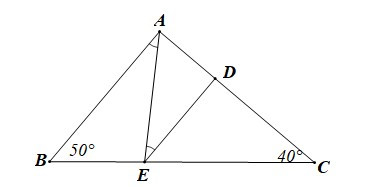
Tam giác CDE là tam giác gì?

A. Tam giác nhọn;

B. Tam giác đều;

C. Tam giác vuông;

D. Tam giác tù.

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác ABC có $\widehat{\mathrm{A}}+\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{A}}=180°-\widehat{\mathrm{B}}-\widehat{\mathrm{C}}$ 

Hay $\widehat{\mathrm{A}}=180°-50°-40°=90°$ 

Xét hai đường thẳng DE và AB có: $\widehat{\mathrm{BAE}}=\widehat{\mathrm{AED}}$ 

Mà hai góc này ở vị trí so le trong

Do đó DE // AB

Suy ra $\widehat{\mathrm{EDC}}=\widehat{\mathrm{A}}$ (hai góc ở vị trí đồng vị)

Mà $\widehat{\mathrm{A}}=90°$ 

Do đó $\widehat{\mathrm{EDC}}=90°$ 

Vậy tam giác CDE là tam giác vuông.

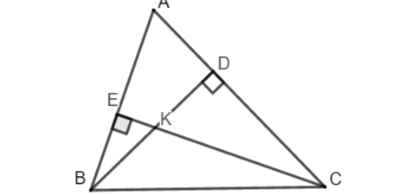
Câu 7:Cho tam giác ABC có , từ B vẻ BD vuông góc với AC, từ C kẻ CE vuông góc với AB, BD cắt CE tại K. Tính số đo góc , biết 

_{Hướng dẫn giải}

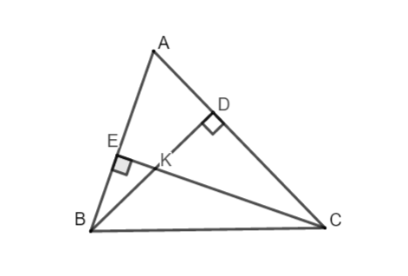
Xét tam giác BCD vuông tại D ta có:

Tương tự xét tam giác BEC vuông tại E có:

Xét tam giác KCB có:

Tổng ba góc của một tam giác bằng  nên ta có:

Do  (đối đỉnh)

Xem thêm các dạng bài tập khác:

60 Bài tập tổng ba góc của một tam giác (có đáp án năm 2023)

50 Bài tập Một số hệ thức về cạnh và góc trong tam giác vuông (có đáp án năm 2023)

60 Bài tập về Góc nhọn, góc tù, góc bẹt (có đáp án năm 2024)

50 Bài tập Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn (có đáp án năm 2024)

70 Bài tập về Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc (có đáp án năm 2024)